Linear Program Polynomial Interpolation Equation

Here goes: remember the statement 'two points determine a line'? The generalization of this statement to polynomials is that '$n+1$ conditions are needed to uniquely determine an $n$-th degree polynomial'. That is, 'three points determine a quadratic', 'four points determine a cubic'. You get the drift. You were given six points: thus, any uniquely determined polynomial that must pass through those six points (you are interpolating, after all) should have a degree at most five (there are polynomials with degree $ 5$ that pass through those points, but you won't be able to pin them down unless you've other conditions). It can happen that the degree of the underlying interpolating polynomial might be less, but there's a way to check for that: take successive differences repeatedly until you encounter a constant sequence ($2.9-0, 14.9-2.8, dots$ and then keep repeating). When I try it out, I've needed five iterations to reach a constant sequence, so an interpolating polynomial of degree $5$ should be expected.
Lecture 19 Polynomial and Spline Interpolation. This equation is linear in these unknowns. Polynomial t requires solving a linear system of equations. Polynomial interpolation is also essential to perform sub-quadratic. Polynomial interpolation defines a linear. If we substitute equation (1). A polynomial) whose graph will pass through a given set of points (x,y). LINEAR INTERPOLATION The simplest form of interpolation is probably the.
However, there is a related procedure, called fitting or regression, that attempts to derive a polynomial of degree usually less than $n$ that is a 'best approximation' of your data. Such a function won't pass through the given points, however, and the underlying assumptions are different.

Interpolation via Gaussian processes is a powerful non-linear interpolation tool. Many popular interpolation tools are actually equivalent to particular Gaussian processes. Gaussian processes can be used not only for fitting an interpolant that passes exactly through the given data points but also for regression, i.e., for fitting a curve through noisy data. In the geostatistics community Gaussian process regression is also known as. Other forms of interpolation Other forms of interpolation can be constructed by picking a different class of interpolants. For instance, rational interpolation is interpolation by using, and is interpolation by using. Another possibility is to use.
The can be used if the number of data points is infinite. Sometimes, we know not only the value of the function that we want to interpolate, at some points, but also its derivative. This leads to problems. When each data point is itself a function, it can be useful to see the interpolation problem as a partial problem between each data point. This idea leads to the problem used in. In higher dimensions.
Bicubic Interpolation in digital signal processing In the domain of digital signal processing, the term interpolation refers to the process of converting a sampled digital signal (such as a sampled audio signal) to that of a higher sampling rate using various digital filtering techniques (e.g., convolution with a frequency-limited impulse signal). In this application there is a specific requirement that the harmonic content of the original signal be preserved without creating aliased harmonic content of the original signal above the original Nyquist limit of the signal (i.e., above fs/2 of the original signal sample rate).
An early and fairly elementary discussion on this subject can be found in Rabiner and Crochiere's book Multirate Digital Signal Processing. Related concepts The term is used to find data points outside the range of known data points. In problems, the constraint that the interpolant has to go exactly through the data points is relaxed. It is only required to approach the data points as closely as possible (within some other constraints).
Polynomial Interpolation Excel
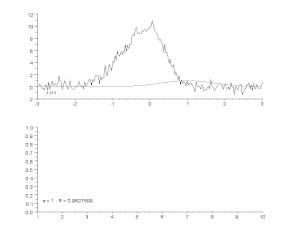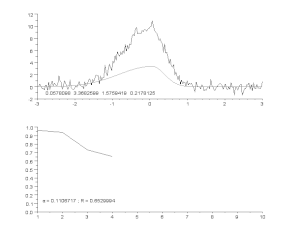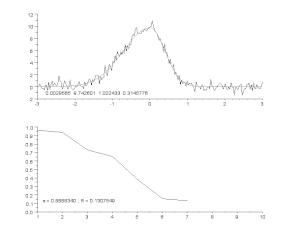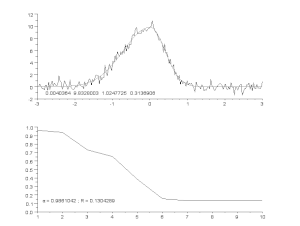
This requires parameterizing the potential interpolants and having some way of measuring the error. In the simplest case this leads to approximation. Studies how to find the best approximation to a given function by another function from some predetermined class, and how good this approximation is. This clearly yields a bound on how well the interpolant can approximate the unknown function. See also.